您提出的问题非常核心，直指 Redis 中 ZSET（有序集合）这一强大数据结构的精髓。为了同时实现您提到的三个特性——元素唯一、元素与分数关联、按分数范围快速查找——ZSET 在底层采用了一种非常精妙的复合数据结构。

核心答案：底层数据结构

Redis 的 ZSET 在底层主要使用了两种数据结构来协同工作：

1. 哈希表 (Hash Table)：用于存储元素（member）和分数（score）的映射关系。
2. 跳表 (Skip List)：用于根据分数对元素进行排序，并支持高效的范围查找。

当一个 ZSET 对象同时满足以下两个条件时，Redis 会采用 ziplist（压缩列表） 进行编码以节省内存：

• 有序集合保存的元素数量小于 128 个；
• 所有元素成员的长度都小于 64 字节。 当任何一个条件不满足时，Redis 就会将编码从 ziplist 转换为 skiplist。 ziplist 是一种内存优化结构，但在大规模数据下，其性能不如 skiplist 和哈希表的组合。因此，我们主要讨论后者，因为它更能体现 ZSET 设计的巧妙之处。

接下来，我们详细解析这两种数据结构如何协同工作，以满足您的所有要求。

---

1. 如何保证元素唯一性？

通过哈希表实现。

• ZSET 的所有元素（member）都存储在一个哈希表中。
• 哈希表的键（key）就是 ZSET 中的元素（member），而值（value）是该元素对应的分数（score）。
• 我们知道，哈希表的键本身就是唯一的。当你尝试向 ZSET 中添加一个已经存在的元素时，Redis 不会插入一个新元素，而是会更新该元素对应的分数。 这正是利用了哈希表键唯一的特性。

操作示例：

• 当你执行 ZADD myzset 10 "redis" 时，哈希表中会创建一个条目 "redis" -> 10。
• 如果你再次执行 ZADD myzset 20 "redis"，哈希表中不会新增条目，而是将 "redis" 对应的值从 10 更新为 20。

这种设计使得通过元素本身查找其分数的操作非常快，时间复杂度为 O(1)，例如 ZSCORE 命令。

2. 如何将元素与分数关联起来？

哈希表与跳表共同实现。

• 哈希表 负责存储从 "元素" 到 "分数" 的直接映射。
• 跳表 则负责存储从 "分数" 到 "元素" 的映射，并且是排序的。

这两者内部通过指针或引用相互关联，确保数据的一致性。当你添加一个元素时，Redis 会同时在哈希表和跳表中进行操作。

• 在哈希表中，它直接存储了 member -> score 的关系。
• 在跳表中，每个节点都保存了元素成员（member）及其分数（score）。

这样一来，ZSET 就同时拥有了两种快速查找的能力：通过元素找分数（O(1)）和通过分数找元素（O(logN)）。

3. 如何实现按分数范围的快速查找？

通过跳表实现。

跳表是一种非常高效的有序数据结构，可以看作是多层级的链表，其查找、插入、删除的平均时间复杂度都是 O(logN)，与平衡二叉树相当，但实现起来更简单。

• 有序性：跳表内部的所有节点都是根据分数从小到大排序的。如果分数相同，则按照元素的字典序进行排序。
• 范围查找：
  1. 当你执行一个按分数范围查找的命令（如 ZRANGEBYSCORE）时，Redis 首先会在跳表中快速定位到范围的起始点。这个定位过程的时间复杂度是 O(logN)。
  2. 一旦找到起始节点，由于跳表的最底层是一个有序的双向链表，Redis 只需要沿着这个链表向后遍历，直到超出范围的结束点即可。 这个遍历过程的复杂度与返回的元素数量（M）成正比，即 O(M)。

因此，一个按分数范围查找操作的总时间复杂度是 O(logN + M)，其中 N 是 ZSET 的总元素数，M 是返回的元素数。这在处理大规模有序数据时非常高效。

总结

特性	实现方式	优势	相关命令示例
元素唯一	哈希表 的键唯一特性	保证了集合中不会有重复的成员。	ZADD, ZSCORE
元素与分数关联	哈希表 和 跳表 共同存储	既能通过元素快速获取分数，也能通过分数找到元素。	ZADD, ZSCORE
按分数范围快速查找	跳表 的有序性和多层结构	能够以对数级时间复杂度定位范围起点，然后高效遍历。	ZRANGEBYSCORE, ZREVRANGEBYSCORE

综上所述，Redis ZSET 通过将哈希表和跳表这两种数据结构的优点结合起来，完美地实现了元素唯一性、成员与分数的映射以及高效的范围查询，使其成为排行榜、实时分析、优先级队列等场景的理想选择。

跳表

好的，没问题。我们来深入剖析一下 Redis 中跳表（Skip List）的精妙之处。

我会从 为什么需要跳表 开始，然后讲解 它的结构，核心操作，最后再分析 Redis 为什么选择它。

---

1. 为什么需要跳表？从有序链表说起

想象一下，为了对元素进行排序，我们最先想到的可能是有序链表。

一个普通的有序链表，所有元素从低到高串联起来：

Header -> 10 -> 21 -> 35 -> 50 -> 78 -> 99 -> Tail

优点：

• 插入和删除时，只需要修改相邻节点的指针，不需要移动大量元素，很方便。
• 天然有序。

致命缺点：

• 查找效率极低。比如我想查找值为 78 的节点，必须从头节点开始，一个一个地向后遍历，直到找到为止。其时间复杂度为 O(N)。当数据量巨大时，这会成为性能瓶颈。

为了解决这个问题，跳表应运而生。它的核心思想就是 “升维”，在原始链表的基础上，增加多级“快速通道”。

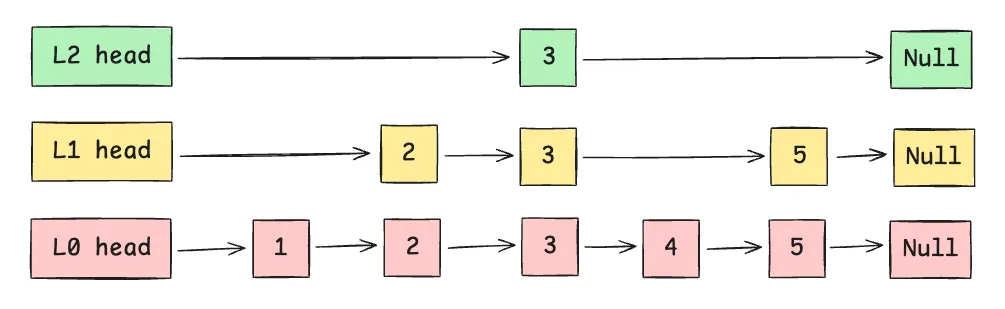
你可以把跳表想象成一个城市的交通网络：

• Level 0 (最底层)：是包含所有站点的“普通公交线路”，站站都停。
• Level 1, Level 2...：是“快速公交”或“地铁线路”，只停靠一些重要的换乘大站。

当你想从城市的一端到另一端时，你肯定会先坐地铁（高层索引）到离你目的地最近的大站，然后再换乘普通公交（底层链表）精确到达。跳表的查找过程就是如此。 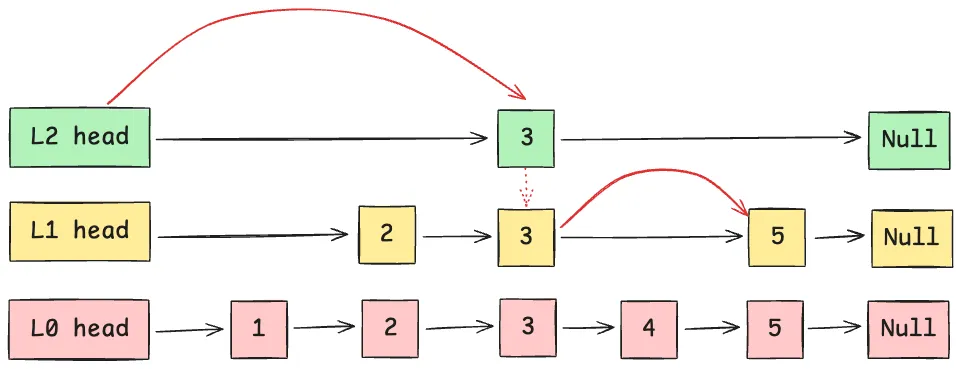跳跃表的多级结构有效地帮助我们跳过节点 1、2 和 4，直接到达 5。相比之下，链表需要遍历所有节点才能到达 5。 上图更是一种概念性表示，旨在使其更易于理解；它并不反映 skiplist 如何实际组织数据。那么，它实际上是如何构建的呢？

2. Redis 跳表的具体结构

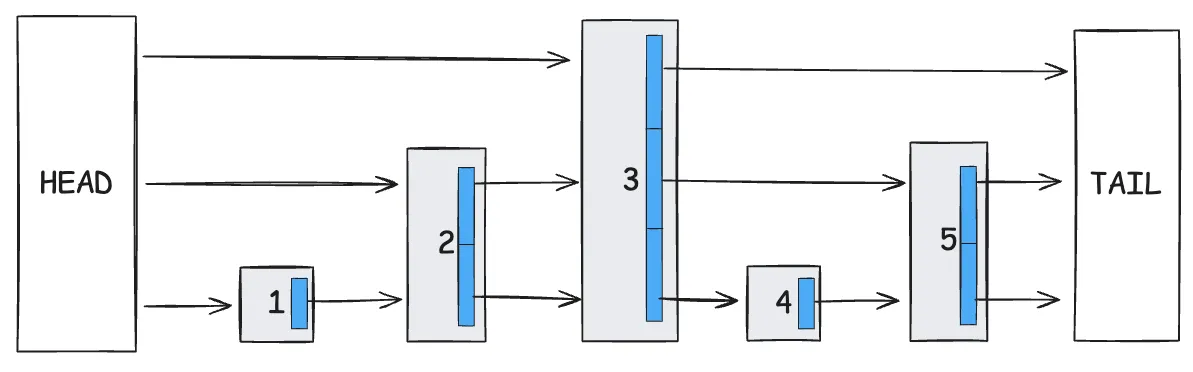实际上，每个节点都有一个指针数组（蓝色），其中的元素指向该节点参与的所有级别的下一个节点。例如，在图中，节点 1 有一个长度为 1 的指针数组，因为它只参与级别 0，而这个指针指向节点 2。

在 Redis 的实现中，一个跳表由两部分构成：zskiplist 和 zskiplistNode。

zskiplistNode (跳表节点)

这是构成跳表的基本单元。每个节点包含以下关键信息：

// Redis 源码中的结构（简化版）
typedef struct zskiplistNode {
    // 元素成员 (member)，在 ZSET 中是一个 sds 对象
    sds ele;
    // 分数 (score)
    double score;
    // 后退指针，用于从后向前遍历
    struct zskiplistNode *backward;
    // 层级信息（柔性数组）
    struct zskiplistLevel {
        // 前进指针，指向同一层的下一个节点
        struct zskiplistNode *forward;
        // 跨度 (span)，表示当前节点到 forward 指向节点之间有多少个节点
        unsigned long span;
    } level[];
} zskiplistNode;

关键点解释：

• ele 和 score：就是 ZSET 中存储的元素和它的分数。跳表根据 score 排序，如果 score 相同，则根据 ele 的字典序排序。
• backward：这是一个指向前一个节点的指针。它使得跳表的最底层构成了一个双向链表，方便从表尾向表头遍历（例如 ZREVRANGE 命令）。
• level[]：这是一个柔性数组，是跳表实现“分层”的核心。一个节点可以同时存在于多个层级。level[0] 存放第一层的前进指针，level[1] 存放第二层的...以此类推。
• span（跨度）：这是 Redis 跳表一个非常精妙的设计。它记录了当前节点的当前层级指针，到下一个节点之间，跨越了多少个底层节点。这个 span 属性是实现 ZRANK (计算排名) 命令时间复杂度为 O(logN) 的关键。

zskiplist (跳表结构体)

这个结构体持有整个跳表的信息：

// Redis 源码中的结构（简化版）
typedef struct zskiplist {
    // 头节点和尾节点指针
    struct zskiplistNode *header, *tail;
    // 跳表中的节点数量
    unsigned long length;
    // 跳表中层级最高的节点的层级数 (不含头节点)
    int level;
} zskiplist;

关键点解释：

• header: 是一个不存储任何实际数据的“哨兵”头节点，它的层级是固定的最高层级（32 或 64），极大地简化了插入和删除的边界条件处理。
• tail: 指向跳表的最后一个节点，方便快速从尾部操作。
• length: 记录了 ZSET 的成员数量，ZCARD 命令可以直接返回这个值，时间复杂度 O(1)。
• level: 记录当前跳表实际达到的最高层级。

---

3. 跳表的核心操作

A. 查找过程 (O(logN))

查找过程是所有操作的基础，我们以查找分数为 50 的节点为例：

1. 从 header 节点的最高层开始。
2. 在当前层，向右移动，直到下一个节点的分数大于等于 50，或者到达了当前层的末尾。
   • 假设在 Level 3，header 的下一个是 99（>50），所以无法前进。
3. 从当前节点下降一层，到 Level 2。
4. 在 Level 2，重复步骤 2。从 header 向右移动，遇到 35（<50），可以前进。在 35 的下一个是 99（>50），无法前进。
5. 从 35 节点下降一层，到 Level 1。
6. 在 Level 1，重复步骤 2。从 35 向右移动，遇到 50（==50），找到了！

整个过程像是在走楼梯，不断地向右、向下，最终精确地定位到目标节点。由于每次都是跳过大量中间节点，其平均时间复杂度为 O(logN)。

B. 插入过程 (O(logN))

1. 确定新节点的层级：Redis 通过一个随机算法为新节点生成一个层级（1 到最大层级之间）。这是一种概率性的平衡策略，使得节点在各层级的分布大致均匀。高层级的节点少，低层级的节点多，形成金字塔结构。
2. 查找插入位置：类似查找操作，找到每一层中新节点应该插入的位置，并记录下这些位置的前驱节点（保存在一个 update 数组中）。
3. 创建并链接节点：创建新节点，然后在 update 数组记录的每个前驱节点后面，将新节点链接进去。同时，还需要更新 backward 指针和所有受影响的 span 值。

在插入新节点时，跳表随机决定它应该占据多少层级。
如果一个节点占据第 3 层，例如，它也会占据第 3 层以下的所有层级，即它占据第 0 层、第 1 层、第 2 层和第 3 层。
这也意味着每个新节点有 100%的概率占据层级 0（否则它会去哪里呢？）。
节点占据更高层级的概率随着层级的增加而减少四倍（即衰减因子=1/4=25%）。具体如下：

• level 0, 100% 层级 0，100%
• level 1, 25% (=100%/4) 层级 1，25%（=100%/4）
• level 2, 6.25% (=25%/4) 第 2 级，6.25%（=25%/4）
• level 3, 1.56% (=6.25%/4) 第 3 级，1.56%（=6.25%/4）
• ...

理论上，随着更多节点的插入，跳表的级数可以无限增长。为了限制内存使用，Redis 将最大级数限制为 32

C. 删除过程 (O(logN))

1. 查找并记录前驱节点：与插入类似，首先找到要删除的节点，并记录下它在每一层的前驱节点。
2. 修改指针和跨度：修改所有前驱节点的 forward 指针，让它们“跳过”被删除的节点，直接指向被删除节点的下一个节点。同时也要更新受影响的 span 值。
3. 释放节点：释放被删除节点的内存。

---

4. Redis 为什么选择跳表而不是平衡树？

像红黑树（Red-Black Tree）这样的平衡二叉搜索树，同样可以实现 O(logN) 的查找、插入、删除，那为什么 Redis 选择了跳表呢？

1. 实现更简单：相对于红黑树复杂的旋转和着色规则，跳表的实现和调试要简单得多。代码可读性和可维护性更高。
2. 范围查找效率相近且更易实现：在跳表中，进行范围查找（如 ZRANGEBYSCORE）非常直观。只需定位到范围的起始点（O(logN)），然后通过底层的双向链表向后遍历即可。在红黑树上做范围查找，需要中序遍历，逻辑相对复杂一些。
3. 支持 O(logN) 的排名查询：通过 span 属性的设计，Redis 的跳表可以非常高效地计算出任意一个元素的排名（ZRANK）。在查找元素的过程中，将沿途经过的所有 span 值累加起来，就是该元素的排名。要在红黑树上实现同等效率的排名查询，需要在每个节点上额外存储其子树的节点数量，这会增加树在旋转时的更新负担和复杂性。
4. 并发场景下更友好 (理论上)：虽然 Redis 本身是单线程模型，但跳表的设计在并发环境中比红黑树更有优势。因为对跳表的修改影响的通常是局部的前后节点，锁定的粒度可以更小。而红黑树的旋转操作可能会影响从叶节点到根节点的整条路径，需要锁定的范围更大。

总结

Redis 的跳表是一种兼具了查找效率（O(logN)）、范围查询便利性和实现简洁性的动态数据结构。它通过随机化的分层思想，巧妙地解决了有序链表查找效率低下的问题，并通过 span 属性的引入，高效地支持了排名查询。正是这种种优点，使其成为实现 ZSET 的理想选择。

希望这次详细的讲解能帮助您更好地理解 Redis 跳表。如果您还有其他问题，请随时提出！

ziplist

继续深入解析一下 Redis 中另一个体现其内存优化艺术的数据结构 —— ziplist（压缩列表）。

ziplist 并非像跳表那样为了追求极致的查找效率，而是为了极致地节省内存。它是 Redis 为哈希（Hash）、列表（List）和有序集合（ZSET）在元素数量较少时提供的一种底层实现。

---

1. 核心思想：是什么与为什么？

是什么？ziplist 本质上不是一个“列表”数据结构，而是一种特殊编码的、连续的内存块（a specially encoded contiguous block of memory）。它将所有元素和元数据紧凑地存储在一起，而不是像传统链表那样通过指针连接分散的节点。

为什么要有 ziplist？ 想象一个标准的双向链表。每个节点除了存储数据外，还需要存储两个指针（prev 和 next）。在 64 位系统中，这两个指针本身就要占用 16 个字节。如果你存储的数据只是一个小整数（比如数字 5），那么为了存储这几个字节的数据，却要付出 16 字节的指针开销，这是巨大的浪费。

ziplist 的设计目标就是消除这种指针开销，用尽可能少的内存来存储一系列小数据。

---

2. ziplist 的内存布局

ziplist 的精髓在于它的内存布局。一个 ziplist 就是一块连续的内存，内部结构如下：

<zlbytes><zltail><zllen><entry-1><entry-2>...<entry-N><zlend>

我们来逐一分解这些部分：

• zlbytes (4 字节):

  • 类型：uint32_t
  • 作用：记录整个 ziplist 所占用的总字节数。
  • 优势：通过这个值，程序可以轻松地知道这块内存区域的边界，方便进行内存的重分配（realloc）。

• zltail (4 字节):

  • 类型：uint32_t
  • 作用：记录从 ziplist 起始地址到最后一个 entry (节点) 的偏移量（offset）。
  • 优势：这个字段使得在列表尾部进行 pop (弹出) 操作的时间复杂度为 O(1)。无需遍历整个列表，直接通过偏移量就能定位到最后一个节点。

• zllen (2 字节):

  • 类型：uint16_t
  • 作用：记录 ziplist 中 entry 的数量。
  • 优势：使得获取列表长度（如 LLEN 命令）的时间复杂度为 O(1)。
  • 注意：当节点数量超过 65535（2^16 - 1）时，这个字段会被置为最大值 65535，此时要获取真实长度就需要遍历整个列表。但在实际使用中，ziplist 根本不会存储这么多元素，所以这基本不成问题。

• entry (可变长度):

  • 这是 ziplist 的核心，每个 entry 代表一个列表中的元素。它的结构非常紧凑，我们稍后详细讲解。

• zlend (1 字节):

  • 类型：uint8_t
  • 作用：一个特殊的结束标记，固定值为 0xFF (二进制 11111111)。
  • 优势：标记 ziplist 的末端，用于遍历时判断是否到达了结尾。

---

3. entry 的内部结构：压缩的艺术

每个 entry 自身也是一个紧凑的结构，由三部分组成：

<previous_entry_length><encoding><content>

• previous_entry_length (前一个节点的长度):

  • 作用：记录了前一个 entry 所占用的总字节数。这个字段是实现从后向前遍历 ziplist 的关键。知道当前节点的地址后，用当前地址减去这个长度，就能得到前一个节点的起始地址。
  • 空间优化: 这个字段本身也是变长的，以节省空间。
    • 如果前一个节点的长度小于 254 字节，那么 previous_entry_length 就用 1 个字节来存储。
    • 如果前一个节点的长度大于或等于 254 字节，那么 previous_entry_length 会用 5 个字节来存储：第 1 个字节固定为 0xFE (254)，后面 4 个字节用于存储实际的长度。

• encoding (编码类型):

  • 作用：决定了紧跟其后的 content 部分存储的是什么类型的数据（字符串还是整数）以及占用了多少字节。
  • 空间优化: 这是 ziplist 压缩的核心。encoding 字段本身也是变长的，通过不同的二进制前缀来表示不同的编码方式。
    • 存储字符串:
      • 如果 encoding 的前两位是 00，表示 content 是一个长度小于等于 63 (2^6-1) 字节的字符串。encoding 本身占 1 字节。
      • 如果前两位是 01，表示 content 是一个长度小于等于 16383 (2^14-1) 字节的字符串。encoding 本身占 2 字节。
      • 如果前两位是 10，表示 content 是一个长度更长的字符串。encoding 本身占 5 字节。
    • 存储整数:
      • 如果 encoding 的前两位是 11，表示 content 存储的是整数。
      • 为了进一步压缩，Redis 定义了多种整数编码，例如：
        • 11110001 到 11111101: content 是一个 1 到 13 之间的小整数，这个整数值直接编码在 encoding 字段的后 4 位，此时 content 字段被省略了，极致节省！
        • 其他 1111xxxx 的值：分别表示 content 是 int16_t, int32_t, int64_t, int24_t 等。

• content (实际内容):

  • 存储元素的实际数据，可以是字节数组（字符串）或整数。其长度和类型由前面的 encoding 字段决定。

---

4. ziplist 的缺点与连锁更新 (Cascading Updates)

ziplist 以其极致的内存效率，牺牲了部分操作的性能，尤其是在更新时。

• 优点：
  • 内存占用极低：没有指针开销，采用变长编码，非常紧凑。
• 缺点：
  • 查找和遍历效率低：无法随机访问，只能从头或从尾开始逐个节点遍历，时间复杂度为 O(N)。
  • 修改操作代价高：每次插入或删除一个元素，都可能需要移动其后的所有元素，涉及大量的内存拷贝，时间复杂度最差为 O(N^2)。
  • 连锁更新风险: 这是 ziplist 最严重的一个潜在问题。

连锁更新 (Cascading Updates)

连锁更新是 ziplist 设计上的一个权衡所带来的最坏情况。

想象一下这个场景：

1. 你有一个 ziplist，里面有一连串的 entry，每个 entry 的长度都刚好是 253 字节。
2. 根据规则，这些 entry 的下一个节点的 <previous_entry_length> 字段都只需要 1 个字节来存储。
3. 现在，你在第一个 entry 的位置插入一个新节点，这个新节点的长度大于等于 254 字节。
4. 这会导致第二个 entry 的 <previous_entry_length> 字段必须从 1 字节扩展到 5 字节。
5. 这个扩展使得第二个 entry 自身的总长度也增加了 4 字节。如果它原来的长度是 253，现在就变成了 257，也跨过了 254 字节的门槛。
6. 因此，第三个 entry 的 <previous_entry_length> 字段也必须从 1 字节扩展到 5 字节...

这个过程就像多米诺骨牌一样，一次简单的插入操作，可能导致后续所有节点都需要进行空间扩展和数据移动，从而引发一次大规模的内存重分配和拷贝，性能急剧下降。

虽然连锁更新在实际场景中发生的概率不高，但它是一个潜在的性能风险。这也是为什么 Redis 严格限制了 ziplist 的大小和元素数量。当超过预设阈值时，Redis 会自动将数据结构从 ziplist 转换为更通用的 linkedlist (对于 List) 或 hashtable + skiplist (对于 Hash 和 ZSET)。

总结

特性	实现方式	优点	缺点
内存效率	连续内存块，变长编码	极致节省内存，无指针开销
头部/尾部操作	zltail 偏移量记录	O(1) 的尾部弹出
长度获取	zllen 字段记录	O(1) 的长度查询
遍历	依赖 previous_entry_length 和计算当前 entry 长度	可以双向遍历	只能顺序遍历，时间复杂度 O(N)
插入/删除	内存重分配 (realloc) 和内存移动 (memmove)		CPU 开销大，最坏可达 O(N^2)，有连锁更新风险

ziplist 是 Redis 在特定场景下（少量、小数据）追求极致内存效率的典范。它体现了在数据结构设计中，空间和时间之间经典的权衡与折中。